Latent-Diffusion-MNIST-DDPM-using-Autoencoder

Latent Diffusion Models for MNIST Dataset using Autoencoders 🌀

Welcome to this project exploring Diffusion Models on the MNIST dataset! 🚀

This repository focuses on generating and reconstructing handwritten digits by integrating:

• Autoencoders with Convolutional Attention Blocks (CABs)
• Denoising Diffusion Probabilistic Models (DDPM) using U-Net

---

Overview

This project aims to reconstruct MNIST digits by encoding them into a latent space and progressively denoising them through a Diffusion Model.

Highlights:

• 🧠 Latent Space Representations - Using attention mechanisms for better feature extraction.
• 🌀 Diffusion Process - Forward and reverse diffusion to model the data distribution.
• 📊 Visualization - Monitoring performance through SSIM/PSNR scores and latent space scatter plots.

---

Autoencoder with CABs

• Encoder compresses MNIST digits into latent representations using convolutional layers and attention.
• Decoder reconstructs the digits from latent space.

Channel Attention Block (CAB)

CABs refine the feature maps by:

• 🌐 Global Average Pooling to extract spatial information.
• 🔄 Two Conv2D Layers to scale the feature channels.
• ✨ Sigmoid Activation to apply attention.

class CALayer(nn.Module):
    def __init__(self, channel, reduction=16, bias=False):
        super(CALayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.conv_du = nn.Sequential(
            nn.Conv2d(channel, channel // reduction, 1, bias=bias),
            nn.ReLU(inplace=True),
            nn.Conv2d(channel // reduction, channel, 1, bias=bias),
            nn.Sigmoid()
        )
    def forward(self, x):
        y = self.avg_pool(x)
        y = self.conv_du(y)
        return x * y

---

Diffusion Model (DDPM)

• 🌪️ Forward Diffusion gradually adds noise to the latent representation.
• 🌟 Reverse Diffusion predicts and removes noise step by step to reconstruct the original image.

U-Net Architecture

The core of the diffusion model is a U-Net, enhanced with:

• Residual Blocks
• Attention Mechanisms
• Time Embeddings for each diffusion step

---

Results and Visualizations

The project features multiple visual outputs that highlight the training and performance of the model.

1. Reconstruction Performance

A side-by-side comparison of original vs reconstructed images. High SSIM and PSNR scores indicate effective reconstructions.

Visualization:

---

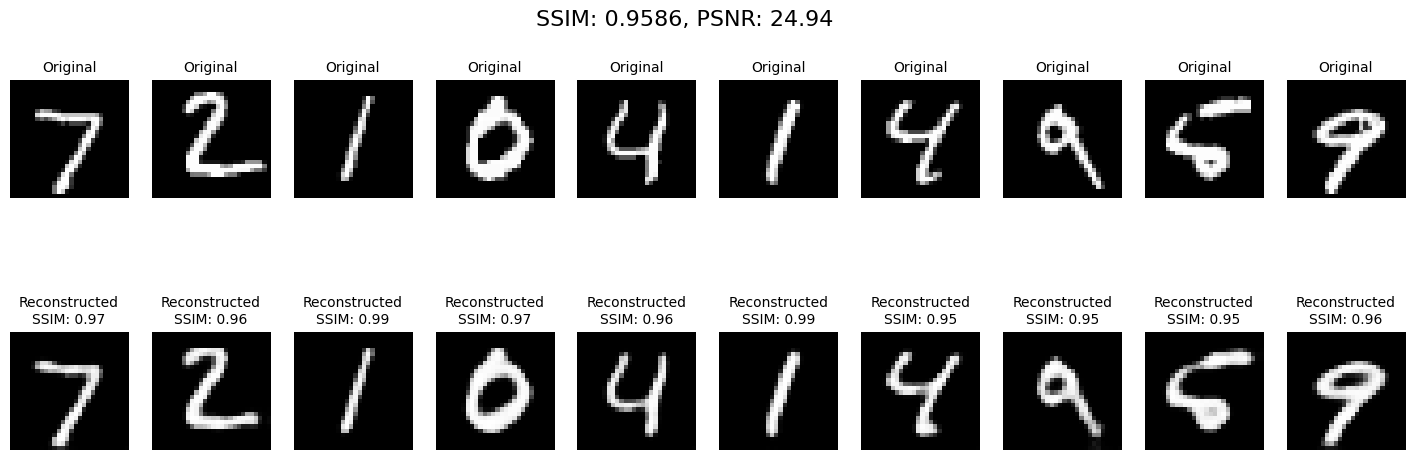
2. Latent Space Visualization

Projection of latent space using t-SNE for a batch and the full test dataset.

Latent Space with Labels (One Batch)

Latent Space (Full Test Dataset)

---

3. Training Loss Curve

Tracking the loss of the diffusion model over epochs.

Loss Plot:

---

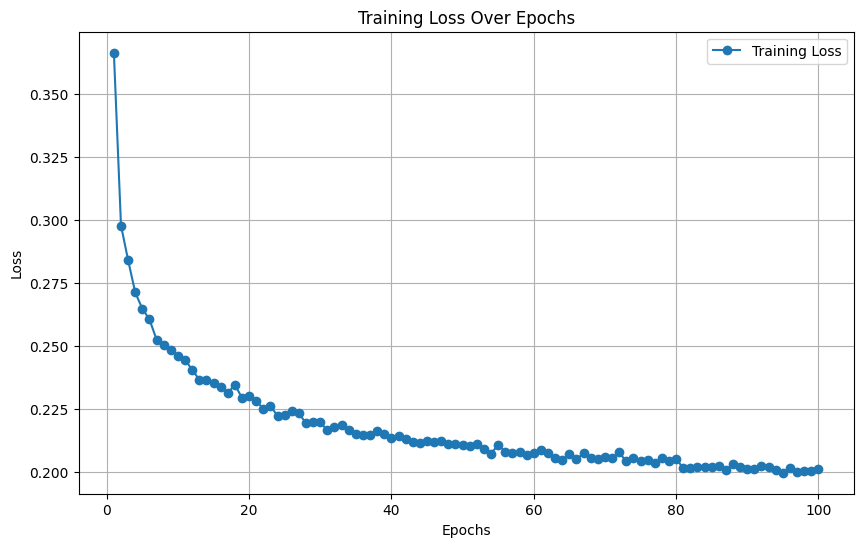
4. Denoising Visualization (Step by Step)

Images progress from noisy states (left) to denoised outputs (right), demonstrating the stepwise denoising process.

Sample Visualization:

---

Formulas and Key Concepts

The project applies unconditional latent diffusion inspired by classic DDPMs but focuses on the latent space. Below is a simplified breakdown of the key concepts:

$x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} ε$

Where:

• (x_t) is the latent at timestep (t)
• (α_t) represents noise schedule
• (ε) is the random noise

Reverse Process (Denoising):

$x_{t-1} = \frac{1}{\sqrt{\alpha_t}} (x_t - (1 - \alpha_t) ε)$

This iterative denoising helps reconstruct the original data.

---

Future Directions

Here are a few ideas to extend this project:

• 🧱 Larger U-Net Models for higher quality image synthesis
• 🔄 Dynamic Diffusion Schedules to speed up convergence
• 📈 Experiment with Other Datasets like Fashion MNIST or CIFAR-10

---

🚀 Happy Training! 🧠